четверг, 8 января 2015 г.

PD №8 - Baza. Macierz wektorowa. Macierz morfizmu. Mnożenie macierzy.

Baza (przestrzeń liniowa)

Bazy w nieskończenie wymiarowych przestrzeniach nazywane są czasami bazami Hamela (jest to częsty zwyczaj w analizie funkcjonalnej). Z drugiej strony, niektórzy matematycy rezerwują nazwę baza Hamela dla dowolnej bazy przestrzeni liczb rzeczywistych jako przestrzeni liniowej nad ciałem liczb wymiernych.

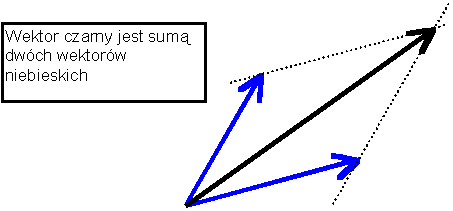
A. Dane są dwie bazy w przestrzeni wektorowej dwu-wymiarowej:

1. {e₁,e₂};

2. {f₁≡e₁+e₂, f₂≡ e₁-e₂}. Wyznaczyć wektor v w bazie {f₁, f₂}

v=2e₁+3e₂≈	2
	3

2	≈x·[f₁]+ y·[f₂]
3

v = x·[e₁+e₂]+y·[ e₁-e₂]

Macierzą rzeczywistą (zespoloną) wymiaru mxn, gdzie m, n Î N nazywamy tablicę prostokątną m × n liczb rzeczywistych (zespolonych) ustawionych w m wierszach i n kolumnach:

Rodzaje macierzy:

*Macierz kwadratowa stopnia n

*Macierz diagonalna stopnia n

*Macierz jednostkowa stopnia n

*Wektor kolumnowy

*Wektor wierszowy

*Macierzą dolnotrójkątną

*Macierz zerowa

Macierz – w matematyce układ liczb, symboli lub wyrażeń zapisanych w postaci prostokątnej tablicy. Choć słowo „macierz” oznacza najczęściej macierz dwuwskaźnikową, to możliwe jest rozpatrywanie macierzy wielowskaźnikowych (zob. notacja wielowskaźnikowa). Macierze jednowskaźnikowe nazywa się często wektorami wierszowymi lub kolumnowymi, co wynika z zastosowań macierzy w algebrze liniowej. W informatyce macierze modeluje się zwykle za pomocą (najczęściej dwuwymiarowych) tablic.
Macierze wprowadza się często jako sposób skondensowanego zapisu układów równań liniowych, co ma na celu wyeliminowanie powtarzających się elementów standardowej notacji układów równań tego rodzaju z wieloma niewiadomymi^[a]. Same układy pojawiają się wprost podczas algebraizacji zagadnień geometrycznych (równania linioweparametryzujące punkty, proste, płaszczyzny itd.). Wyrosłym na tym gruncie, podstawowym przeznaczeniem macierzy jest jednak sformułowanie spójnego, a zarazem zwartego sposobu zapisu pojęć i twierdzeń algebry liniowej, a więc przede wszystkim opisuprzekształceń liniowych między dwoma przestrzeniami liniowymi nad wspólnym ciałem(skończeniewymiarowych, z ustalonymi bazami), czy form dwuliniowych na przestrzeni liniowej (skończonego wymiaru z wybraną bazą). Nieomalże wszystkie inne zastosowania wynikają z tych interpretacji − macierz Jacobiego, macierz Hessego, czy gradient obecne w analizie wielowymiarowej to macierze pochodnych (przedstawiane w ustalonych bazach, zwykle standardowych); podobnie ma się rzecz z wieloma możliwościami rozkładu macierzyna iloczyn macierzy o ustalonych własnościach − odpowiadają one złożeniom odpowiednich przekształceń. Macierze bada się również niezależnie od jakichkolwiek zastosowań (rozwijając w ten sposób dostępny aparat pojęciowy); samodzielny dział matematyki im poświęcony nazywa się teorią macierzy.

C.Obliczanie.

A·A=A²=	3 -1	·	3 -1	=	3·3+(-1)·(-2) 3·(-1)+(-1)·4
	-2 4		-2 4		-2·3+4·(-2) -2·(-1)+4·4

A·A=A²=	11 -7
	-14 18

A²·A=	11 -7	·	3 -1	=	11·3+(-7)·(-2) 11·(-1)+(-7)·4
	-14 18		-2 4		-14·3+18·(-2) -14·(-1)+18·4

A²·A=	47 -39
	-78 86

A·A²=	3 -1	·	11 -7	=	3·11+(-1)·(-14) 3·(-7)+(-1)·18
	-2 4		-14 18		-2·11+4·(-14) -2·(-7)+4·18

A·A²=	47 -39
	-78 86

A²·A= A·A²=A³

среда, 7 января 2015 г.

PD №7 - Dwoistość=Dualność. Dual R-module and dual (sprzężona) R-space.

Dwa rodzaje wektorów.
Dwoistość - To znaczy gdy jedno nie istnieje bez drugiego (Bez wody nie ma ryb).Naprzyklad jak wektory i formy.Dla nich istnieje ewaluacja, która nadaje im wartość skalarną.
Przyklad ewaluacji: [trawa, czlowiek] ----> ewaluacja to koszenie trawy ----> siano

B. Podprzestrzeń - to podzbiór danej przestrzeni, która sama ma tę samą co ona (przestrzeń) strukturą lub własności.

ker α={v∈V, αv=0∈R}

ker α=0wektor

ker α= podprzestrzeń 1-wymiarowa

i, gdy αv = 0 i αu = 0 to wtedy α(v + u) = 0, to jest grzbiet formy.

C. Gdy αv = 0 i βv = 0, wtedy (α + β)v = 0 to oznacza, że ker v jest podprzestrzenią form.

Graficzne dodawanie form:

g₁v=(i⊗i+j⊗j)(4i+3j)=i(4i+3j)i+j(4i+3j)j=4i+3j |v|²=(g₁v)v=(4i+3j)(4i+3j)=16+0+0+9=25
g₂v=(i⊗j+j⊗i)(4i+3j)=i(4i+3j)j+j(4i+3j)i=4j+3i |v|²=(g₂v)v=(4j+3i)(4i+3j)=0+12+12+0=24

(g1) lepiej

вторник, 6 января 2015 г.

PD №6 - Przestrzeń liniowa/wektorowa. Dodawanie i tenzorowe mnożenie przestrzeni wektorowych.

host

Przestrzeń liniowa lub wektorowa – w matematyce zbiór obiektów (nazywanych "wektorami"), które mogą być, nieformalnie rzecz ujmując, skalowane i dodawane. Formalnie jest to zbiór z określonymi dwoma działaniami: dodawaniem elementów tej przestrzeni (wektorów) i mnożeniem przez elementy ustalonego ciała, które związane są ze sobą poniższymi aksjomatami. Przestrzenie liniowe to podstawowy obiekt badań algebry liniowej i analizy funkcjonalnej. Znajdują zastosowanie niemal we wszystkich gałęziach matematyki, naukach ścisłych i inżynierii.

Morfizmy przestrzeni liniowych MOZNO dodawac zawsze!

6 A.

Niech a,b,c ϵ R, gdzie R-zbiór liczb rzeczywistych oraz jest pierścieniem przemiennym.
a·(b+c)=a·b+a·c ϵ R. Endo-morfizm jest odwzorowanie na siebie. Tutaj a,b,c są w pierścieniu R, oraz otrzymany wynik również jest w tym samym pierścieniu. Zatem dystrybutywność w pierścieniu skalarów jest endomorfizmem grupy addytywnej pierścienia.

6 B.

dimz2Z2=1

dimz2(Z2 + Z2)=dimz2Z2 + dimz2Z2=1 + 1=2

dimz2(Z2 x Z2)=dimz2Z2 x dimz2Z2=1 x 1=1

6 C.

1. Morfizmy pierścieni nie można dodawać.

Weźmy dwa dowolne morfizmy pierścieni f i h:

f(r₁·r₂)=(fr₁)·(fr₂)

h(r₁·r₂)=(hr₁)·(hr₂)

(f+h)( r₁·r₂)≠[(f+h)r₁]·[(f+h)r₂]

f (r₁r₂)+ h (r₁r₂)≠(fr₁+hr₁)·(fr₂+hr₂)

(fr₁)·(fr₂)+ (hr₁)·(hr₂) ≠(fr₁+hr₁)·(fr₂+hr₂)

Nie ma równości!

2. Morfizmy przestrzeni/modułów można dodawać.

Weźmy dwa dowolne morfizmy przestrzeni f i h, gdzie r-to skalar, a v-to wektor:

f(r·v)=r·(fv)

h(r·v)=r·(hv)

(f+h)( r·v)=r·(f+h)(v)

f (r·v)+ h (r·v)= r·(fv+hv)

r·(fv)+ r·(hv)= r·(fv+hv)

r·(fv+hv)= r·(fv+hv)

Jest równość!

6 D.

Transformacja Galileusza – jest to transformacja współrzędnych przestrzennych i czasu z jednego układu odniesienia do innego, poruszającego się ruchem jednostajnym prostoliniowym względem pierwszego.Rozumowanie Galileusza wespół z koncepcją absolutnego czasu, płynącego tak samo dla wszystkich obserwatorów, prowadzi do transformacji, która pozwala przeliczyć te same obserwacje dla różnych układów odniesienia. Transformacja Galileusza prowadzi do wniosku, że prędkości postrzegane przez różnych obserwatorów nie muszą być takie same, ale niezmienne pozostają odległości między punktami i odstępy czasu pomiędzy wydarzeniami.

Szczególna teoria względności

Transformacja ta wydaje się bardzo naturalna, lecz jest niezgodna z równaniami Maxwella, co przejawia się w zmianie wartości prędkości światła przy zmianie układu odniesienia. Na przykład jeśli światło według obserwatora O porusza się wzdłuż osi OX w kierunku dodatnim tej osi z prędkością c, to według obserwatora O' ma ono prędkość c - v. Ponieważ doświadczalne poszukiwania takiej zmiany zakończyły się fiaskiem (doświadczenie Michelsona-Morleya), należy przyjąć, że istnieje sprzeczność pomiędzy doświadczeniem z dziedziny elektromagnetyzmu a stosowaniem transformacji Galileusza.

Rozwiązaniem tego problemu była sformułowana przez Alberta Einsteina szczególna teoria względności, która postuluje zmianę praw transformacyjnych dla dużych prędkości układów odniesienia. W teorii tej wykorzystywane są transformacje Lorentza. Poza światem cząstek subatomowych czy prędkości porównywalnych do prędkości światła transformacja Galileusza jest wystarczającym przybliżeniem ogólniejszej teorii – szczególnej teorii względności. W codziennym życiu nie mamy możliwości zaobserwowania jej efektów ponieważ niemożliwe jest obserwowanie osiągnięcia prędkości bliskich prędkości światła dla obiektów makroskopowych (samochód, samolot, przedmioty codziennego użytku).

6 E.

Tensor, wielkość tensorowa, obiekt geometryczny – obiekt matematyczny będący uogólnieniem pojęcia wektora.

Zbiór wszystkich tensorów wraz z odpowiednimi działaniami nazywamy przestrzenią tensorową. Przestrzeń tensorowa jest sumą prostą przeliczalnej liczby przestrzeni liniowych.

Definicja

Niech

V

będzie przestrzenią liniową nad ciałem

K

V^*

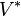będzie przestrzenią do niej sprzężoną oraz niech

p

q

będą nieujemnymi liczbami całkowitymi. Rozważmy iloczyn kartezjański

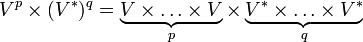V^p\times (V^*)^q = \underbrace{V\times \ldots \times V}_p \times \underbrace{V^*\times \ldots \times V^*}_q

Każde odwzorowanie (p+q)-liniowe

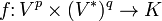
f\colon V^p\times (V^*)^q\to K

nazywane jest tensorem na

V

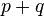(typu (p, q) i rzędu $p+q$ ) p-krotnie kowariantnym i q-krotnie kontrawariantnym. Dla

p=0

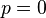mówi się o tensorze kontrawariantnym a dla

q=0

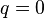, o tensorze kowariantnym. Przyjmuje się, że tensory typu (0,0) to skalary (elementy ciała

K

Zbiór

\mathbb{T}^p_q(V)

wszystkich tensorów typu

(p, q)

V

tworzy przestrzeń liniową z działaniami określonymi punktowo.

понедельник, 5 января 2015 г.

PD №4 - (Homo)-Morfizmy grup i piercieni

A. Jaka jest roznica miedzy (homo)morfizmem grup i (homo)morfizmem pierscieni?

Homo-morfizm grup – w teorii grup funkcja odwzorowująca grupę w grupę, czyli przekształcenie zachowujące strukturę tych algebr.

Homo-morfizm pierścieni to, nieformalnie, przekształcenie z jednego pierścienia w drugi zachowujące strukturę.

Niech

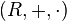(R, +, \cdot)

oraz

(S, \oplus, \odot)

będą dowolnymi pierścieniami.

Homomorfizmem pierścieni

R

S

nazywamy dowolne odwzorowanie

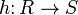h\colon R \to S

takie, że

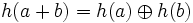$h(a + b) = h(a) \oplus h(b)$ oraz
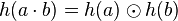$h(a \cdot b) = h(a) \odot h(b)$ .

DefinicjaNiech G, F będą grupami.
(1) Odwzorowanie φ : G → F nazywamy homomorfizmem, jeśli
∀a, b ∈ G[φ(a · b) = f(a) · f(b)].
Zbiór wszystkich homomorfizmów grupy G w grupę F oznaczamy Hom(G, F).
(2) Homomorfizm φ : G → F nazywamy monomorfizmem, jeśli jest różnowartościowy.
(3) Homomorfizm φ : G → F nazywamy epimorfizmem, jeśli jest surjektywny.
(4) Homomorfizm φ : G → G nazywamy endomorfizmem. Zbiór wszystkich endomorfizmów oznaczamy
End(G).
(5) Izomorfizm φ : G → G nazywamy automorfizmem. Zbiór wszystkich automorfizmów oznaczamy
Aut(G).
(6) Jeśli φ : G → F jest homomorfizmem, to zbiór
ker φ = φ−1
(1F ) = {a ∈ G : φ(a)=1F }
nazywamy jądrem homomorfizmu φ, zaś zbiór
imφ = φ(G) = {b ∈ F : ∃a ∈ g[b = φ(a)]}
nazywamy obrazem homomorfizmu φ.
Niech G, F będą grupami, niech φ : G → F będzie homomorfizmem. Wówczas:
(1) φ(1G)=1F ;
(2) φ(a−1)=(φ(a))−1, dla a ∈ G;
(3) φ(ak)=(φ(a))k, dla a ∈ G;
(4) r(φ(a))|r(a), dla a ∈ G;
(5) jeśli φ jest izomorfizmem, to r(φ(a)) = r(a), dla a ∈ G.
Dowód. (1) Mamy:
φ(1G) = φ(1G · 1G) = φ(1G)φ(1G),
skąd, po skróceniu, φ(1G)=1G.
(2) Mamy:
1F = φ(1G) = φ(a · a−1
) = φ(a)φ(a−1
),
skąd, po podzieleniu, φ(a−1)=(φ(a))−1.
(3) Prosty dowód indukcyjny pozostawiamy Czytelnikowi jako nietrudne ćwiczenie.
(4) Niech r(a) = k. Wówczas ak = 1G i stąd
1F = φ(1G) = φ(ak)=(φ(a))k.
Zatem r(φ(a))|r(a).
(5) Odwzorowanie φ : G → F jest różnowartościowe i surjektywne, więc istnieje odwzorowanie
odwrotne φ−1 : F → G. W szczególności
r(φ(a))|r(a) oraz r(φ−1
(φ(a))) = r(a)|r(φ(a)).
Zatem r(φ(a)) = r(a).

B. Esej o klasyfikacji-terminologii morfizmow.

Homo-morfizm - (grec. homo-podobny, taki samy). Homomorfizm oznacza odwzorowanie jednej struktury algebroicznej w drugą, zachowując przy tym strukturę i odpowiadające sobie operacje. I to odwzorowanie jest podobne do tych struktur algebroicznych.

Endo-morfizm - homomorfizm, który odwzorowuje system algebroiczny w siebie, czyli w swój podsystem. Endo - wewnętrzny.

Epi-morfizm - jednoznaczne odwzorowanie jednego systemu algebraicznego na inny. Posiada prawostronną własność skracania. Epi- prawy.

Mono-morfizm - przekształcenie różnowartościowe, posiada lewostronną własność skracania. Mono- lewy.

Izo-morfizm - morfizm, który posiada lewą i prawą odwrotność, jest jednocześnie epimorfizmem i monomorfizmem, i te odwrotności są równoważne. Izo- równy.

*Morfizm posiada jadro.
*Morfizmy pierscieni NIE mozno dodawac!

воскресенье, 4 января 2015 г.

PD №3 - Ideały w pierścieniach

Ideał – w algebrze abstrakcyjnej, podzbiór pierścienia o własnościach pozwalających na konstrukcję pierścienia ilorazowego. Pojęcie ideału zostało wprowadzone przezDedekinda jako uogólnienie pojęcia liczby idealnej, rozważanego przez Kummera. Badania Dedekinda były kontynuowane przez Hilberta i, szczególnie, przez Emmę Noether.

DEFINICJA

Ideałem pierścienia przemiennego

R

nazywa się każdy podzbiór $I \sub R$ taki, że:

$I\;$ jest podgrupą grupy addytywnej pierścienia
jeśli $\gamma \in R$ oraz $\alpha \in I$ , to $\gamma\cdot\alpha \in I$

Zamiast pierwszego warunku wystarczy przyjąć, że zbiór

I

jest niepusty oraz, że spełniony jest warunek następujący:

jeśli $\alpha, \beta \in I$ , to $\alpha - \beta \in I.$

Niekiedy nie zakłada się przemienności pierścienia

R

. Wtedy powyższe warunki definiują ideał lewostronny pierścienia, natomiast jeśli zastąpimy drugi warunek następującym:

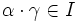
jeśli $\gamma \in R$ oraz $\alpha \in I$ , to $\alpha\cdot\gamma \in I$

to otrzymamy definicję ideału prawostronnego.

Jeżeli

A

jest dowolnym podzbiorem pierścienia

R

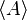, to przez $\langle A\rangle$ oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia

R

zawierający zbiór

A

. Można udowodnić, że

$\langle A\rangle=\{r_1a_1+\ldots+r_na_n: r_i\in R, a_i\in A, n\in \mathbb N\}$

Przyklad Podpierścienia

Definicja

m Z ∋ mk, ml

(mk)(ml)=m(kml)∈ Z

mk+ml=m(k+l)∈ mZ

W ciele (pierścieniu) liczb rzeczywistych istnieje podpierścień izomorficzny z ciałem (pierścieniem) liczb wymiernych.
Podobnie w pierścieniu liczb wymiernych istnieje podpierścień izomorficzny z pierścieniem liczb całkowitych.
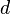Jeśli $d$ jest bezkwadratową liczbą całkowitą, to $\mathbb Z\left[\sqrt d\right] = \{ a+b\sqrt{d} : a,b\in\mathbb Z \}$ jest podpierścieniem ciała liczb zespolonych.

Idealy

W dowolnym pierścieniu zbiór $\{0\}$ jest ideałem, zwanym trywialnym.
Zbiór wszystkich elementów pierścienia $R$ jest ideałem w tym pierścieniu (zwanym niewłaściwym).
W pierścieniu $\mathbb Z$ liczb całkowitych przykładem ideału jest zbiór wszystkich liczb parzystych. Ideałem jest również zbiór wszystkich liczb podzielnych przez 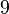$9$ . Ogólniej, każdy ideał pierścienia $\mathbb Z$ jest zbiorem wszystkich liczb podzielnych przez pewną liczbę naturalną $k$ . Zatem $\mathbb Z$ jest pierścieniem ideałów głównych. Ideał pierścienia $\mathbb Z$ jest pierwszy, wtedy i tylko wtedy, gdy jest zbiorem liczb podzielnych przez pewną liczbę pierwszą.
Jedynymi ideałami dowolnego ciała są ideał trywialny (złożony z samego zera) i niewłaściwy (całe ciało).
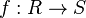Jeśli $f: R \to S$ jest homomorfizmem pierścieni, to jego jądro $\ker f$ jest ideałem w pierścieniu $R$ .
Zbiór elementów nieodwracalnych pierścienia $R$ tworzy ideał wtedy i tylko wtedy, gdy $R$ zawiera dokładnie jeden ideał maksymalny.