Ideał – w algebrze abstrakcyjnej, podzbiór pierścienia o własnościach pozwalających na konstrukcję pierścienia ilorazowego. Pojęcie ideału zostało wprowadzone przezDedekinda jako uogólnienie pojęcia liczby idealnej, rozważanego przez Kummera. Badania Dedekinda były kontynuowane przez Hilberta i, szczególnie, przez Emmę Noether.
DEFINICJA
Ideałem pierścienia przemiennego R nazywa się każdy podzbiór 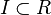 taki, że:
taki, że:
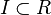 taki, że:
taki, że: jest podgrupą grupy addytywnej pierścienia
jest podgrupą grupy addytywnej pierścienia- jeśli
 oraz
oraz  , to
, to 
Zamiast pierwszego warunku wystarczy przyjąć, że zbiór I jest niepusty oraz, że spełniony jest warunek następujący:
- jeśli
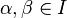 , to
, to 
Niekiedy nie zakłada się przemienności pierścienia R. Wtedy powyższe warunki definiują ideał lewostronny pierścienia, natomiast jeśli zastąpimy drugi warunek następującym:
- jeśli
 oraz
oraz  , to
, to 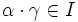
to otrzymamy definicję ideału prawostronnego.
Jeżeli A jest dowolnym podzbiorem pierścienia R, to przez 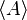 oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia R zawierający zbiór A. Można udowodnić, że
oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia R zawierający zbiór A. Można udowodnić, że
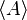 oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia R zawierający zbiór A. Można udowodnić, że
oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia R zawierający zbiór A. Można udowodnić, że
Przyklad Podpierścienia
- Definicja
- m Z ∋ mk, ml
- (mk)(ml)=m(kml)∈ Z
- mk+ml=m(k+l)∈ mZ
- W ciele (pierścieniu) liczb rzeczywistych istnieje podpierścień izomorficzny z ciałem (pierścieniem) liczb wymiernych.
- Podobnie w pierścieniu liczb wymiernych istnieje podpierścień izomorficzny z pierścieniem liczb całkowitych.
- Jeśli
 jest bezkwadratową liczbą całkowitą, to
jest bezkwadratową liczbą całkowitą, to ![\mathbb Z\left[\sqrt d\right] = \{ a+b\sqrt{d} : a,b\in\mathbb Z \}](https://upload.wikimedia.org/math/2/8/6/28614ac91fe710577690f0e43184b68a.png) jest podpierścieniem ciała liczb zespolonych.
jest podpierścieniem ciała liczb zespolonych.
Idealy
- W dowolnym pierścieniu zbiór
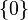 jest ideałem, zwanym trywialnym.
jest ideałem, zwanym trywialnym. - Zbiór wszystkich elementów pierścienia
 jest ideałem w tym pierścieniu (zwanym niewłaściwym).
jest ideałem w tym pierścieniu (zwanym niewłaściwym). - W pierścieniu
 liczb całkowitych przykładem ideału jest zbiór wszystkich liczb parzystych. Ideałem jest również zbiór wszystkich liczb podzielnych przez
liczb całkowitych przykładem ideału jest zbiór wszystkich liczb parzystych. Ideałem jest również zbiór wszystkich liczb podzielnych przez 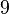 . Ogólniej, każdy ideał pierścienia
. Ogólniej, każdy ideał pierścienia  jest zbiorem wszystkich liczb podzielnych przez pewną liczbę naturalną
jest zbiorem wszystkich liczb podzielnych przez pewną liczbę naturalną  . Zatem
. Zatem  jest pierścieniem ideałów głównych. Ideał pierścienia
jest pierścieniem ideałów głównych. Ideał pierścienia  jest pierwszy, wtedy i tylko wtedy, gdy jest zbiorem liczb podzielnych przez pewną liczbę pierwszą.
jest pierwszy, wtedy i tylko wtedy, gdy jest zbiorem liczb podzielnych przez pewną liczbę pierwszą. - Jedynymi ideałami dowolnego ciała są ideał trywialny (złożony z samego zera) i niewłaściwy (całe ciało).
- Jeśli
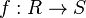 jest homomorfizmem pierścieni, to jego jądro
jest homomorfizmem pierścieni, to jego jądro  jest ideałem w pierścieniu
jest ideałem w pierścieniu  .
. - Zbiór elementów nieodwracalnych pierścienia
 tworzy ideał wtedy i tylko wtedy, gdy
tworzy ideał wtedy i tylko wtedy, gdy  zawiera dokładnie jeden ideał maksymalny.
zawiera dokładnie jeden ideał maksymalny.
- W dowolnym pierścieniu zbiór
-

Комментариев нет:
Отправить комментарий