host
Przestrzeń liniowa lub wektorowa – w matematyce zbiór obiektów (nazywanych "wektorami"), które mogą być, nieformalnie rzecz ujmując, skalowane i dodawane. Formalnie jest to zbiór z określonymi dwoma działaniami: dodawaniem elementów tej przestrzeni (wektorów) i mnożeniem przez elementy ustalonego ciała, które związane są ze sobą poniższymi aksjomatami. Przestrzenie liniowe to podstawowy obiekt badań algebry liniowej i analizy funkcjonalnej. Znajdują zastosowanie niemal we wszystkich gałęziach matematyki, naukach ścisłych i inżynierii.
Przestrzeń liniowa lub wektorowa – w matematyce zbiór obiektów (nazywanych "wektorami"), które mogą być, nieformalnie rzecz ujmując, skalowane i dodawane. Formalnie jest to zbiór z określonymi dwoma działaniami: dodawaniem elementów tej przestrzeni (wektorów) i mnożeniem przez elementy ustalonego ciała, które związane są ze sobą poniższymi aksjomatami. Przestrzenie liniowe to podstawowy obiekt badań algebry liniowej i analizy funkcjonalnej. Znajdują zastosowanie niemal we wszystkich gałęziach matematyki, naukach ścisłych i inżynierii.
Morfizmy przestrzeni liniowych MOZNO dodawac zawsze!
6 A.
Niech a,b,c ϵ R, gdzie R-zbiór liczb rzeczywistych oraz jest pierścieniem przemiennym.
a·(b+c)=a·b+a·c ϵ R. Endo-morfizm jest odwzorowanie na siebie. Tutaj a,b,c są w pierścieniu R, oraz otrzymany wynik również jest w tym samym pierścieniu. Zatem dystrybutywność w pierścieniu skalarów jest endomorfizmem grupy addytywnej pierścienia.
a·(b+c)=a·b+a·c ϵ R. Endo-morfizm jest odwzorowanie na siebie. Tutaj a,b,c są w pierścieniu R, oraz otrzymany wynik również jest w tym samym pierścieniu. Zatem dystrybutywność w pierścieniu skalarów jest endomorfizmem grupy addytywnej pierścienia.
6 B.
dimz2Z2=1
dimz2(Z2 + Z2)=dimz2Z2 + dimz2Z2=1 + 1=2
dimz2(Z2 x Z2)=dimz2Z2 x dimz2Z2=1 x 1=1
6 C.
1. Morfizmy pierścieni nie można dodawać.
Weźmy dwa dowolne morfizmy pierścieni f i h:
f(r1·r2)=(fr1)·(fr2)
h(r1·r2)=(hr1)·(hr2)
(f+h)( r1·r2)≠[(f+h)r1]·[(f+h)r2]
f (r1r2)+ h (r1r2)≠(fr1+hr1)·(fr2+hr2)
(fr1)·(fr2)+ (hr1)·(hr2) ≠(fr1+hr1)·(fr2+hr2)
Nie ma równości!
2. Morfizmy przestrzeni/modułów można dodawać.
Weźmy dwa dowolne morfizmy przestrzeni f i h, gdzie r-to skalar, a v-to wektor:
f(r·v)=r·(fv)
h(r·v)=r·(hv)
(f+h)( r·v)=r·(f+h)(v)
f (r·v)+ h (r·v)= r·(fv+hv)
r·(fv)+ r·(hv)= r·(fv+hv)
r·(fv+hv)= r·(fv+hv)
Jest równość!
6 D.
Transformacja Galileusza – jest to transformacja współrzędnych przestrzennych i czasu z jednego układu odniesienia do innego, poruszającego się ruchem jednostajnym prostoliniowym względem pierwszego.Rozumowanie Galileusza wespół z koncepcją absolutnego czasu, płynącego tak samo dla wszystkich obserwatorów, prowadzi do transformacji, która pozwala przeliczyć te same obserwacje dla różnych układów odniesienia. Transformacja Galileusza prowadzi do wniosku, że prędkości postrzegane przez różnych obserwatorów nie muszą być takie same, ale niezmienne pozostają odległości między punktami i odstępy czasu pomiędzy wydarzeniami.
Szczególna teoria względności
Transformacja ta wydaje się bardzo naturalna, lecz jest niezgodna z równaniami Maxwella, co przejawia się w zmianie wartości prędkości światła przy zmianie układu odniesienia. Na przykład jeśli światło według obserwatora O porusza się wzdłuż osi OX w kierunku dodatnim tej osi z prędkością c, to według obserwatora O' ma ono prędkość c - v. Ponieważ doświadczalne poszukiwania takiej zmiany zakończyły się fiaskiem (doświadczenie Michelsona-Morleya), należy przyjąć, że istnieje sprzeczność pomiędzy doświadczeniem z dziedziny elektromagnetyzmu a stosowaniem transformacji Galileusza.
Rozwiązaniem tego problemu była sformułowana przez Alberta Einsteina szczególna teoria względności, która postuluje zmianę praw transformacyjnych dla dużych prędkości układów odniesienia. W teorii tej wykorzystywane są transformacje Lorentza. Poza światem cząstek subatomowych czy prędkości porównywalnych do prędkości światła transformacja Galileusza jest wystarczającym przybliżeniem ogólniejszej teorii – szczególnej teorii względności. W codziennym życiu nie mamy możliwości zaobserwowania jej efektów ponieważ niemożliwe jest obserwowanie osiągnięcia prędkości bliskich prędkości światła dla obiektów makroskopowych (samochód, samolot, przedmioty codziennego użytku).
6 E.
Tensor, wielkość tensorowa, obiekt geometryczny – obiekt matematyczny będący uogólnieniem pojęcia wektora.
Zbiór wszystkich tensorów wraz z odpowiednimi działaniami nazywamy przestrzenią tensorową. Przestrzeń tensorowa jest sumą prostą przeliczalnej liczby przestrzeni liniowych.
Definicja
Niech  będzie przestrzenią liniową nad ciałem
będzie przestrzenią liniową nad ciałem  ,
, 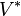 będzie przestrzenią do niej sprzężoną oraz niech
będzie przestrzenią do niej sprzężoną oraz niech  i
i  będą nieujemnymi liczbami całkowitymi. Rozważmy iloczyn kartezjański
będą nieujemnymi liczbami całkowitymi. Rozważmy iloczyn kartezjański
 będzie przestrzenią liniową nad ciałem
będzie przestrzenią liniową nad ciałem  ,
, 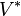 będzie przestrzenią do niej sprzężoną oraz niech
będzie przestrzenią do niej sprzężoną oraz niech  i
i  będą nieujemnymi liczbami całkowitymi. Rozważmy iloczyn kartezjański
będą nieujemnymi liczbami całkowitymi. Rozważmy iloczyn kartezjański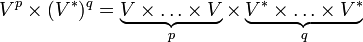 .
.
Każde odwzorowanie (p+q)-liniowe
nazywane jest tensorem na  (typu (p, q) i rzędu
(typu (p, q) i rzędu 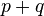 ) p-krotnie kowariantnym i q-krotnie kontrawariantnym. Dla
) p-krotnie kowariantnym i q-krotnie kontrawariantnym. Dla 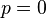 mówi się o tensorze kontrawariantnym a dla
mówi się o tensorze kontrawariantnym a dla 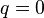 , o tensorze kowariantnym. Przyjmuje się, że tensory typu (0,0) to skalary (elementy ciała
, o tensorze kowariantnym. Przyjmuje się, że tensory typu (0,0) to skalary (elementy ciała  ).
).
 (typu (p, q) i rzędu
(typu (p, q) i rzędu 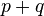 ) p-krotnie kowariantnym i q-krotnie kontrawariantnym. Dla
) p-krotnie kowariantnym i q-krotnie kontrawariantnym. Dla 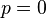 mówi się o tensorze kontrawariantnym a dla
mówi się o tensorze kontrawariantnym a dla 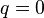 , o tensorze kowariantnym. Przyjmuje się, że tensory typu (0,0) to skalary (elementy ciała
, o tensorze kowariantnym. Przyjmuje się, że tensory typu (0,0) to skalary (elementy ciała  ).
).
Zbiór  wszystkich tensorów typu
wszystkich tensorów typu  na
na  tworzy przestrzeń liniową z działaniami określonymi punktowo.
tworzy przestrzeń liniową z działaniami określonymi punktowo.
 wszystkich tensorów typu
wszystkich tensorów typu  na
na  tworzy przestrzeń liniową z działaniami określonymi punktowo.
tworzy przestrzeń liniową z działaniami określonymi punktowo.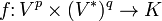
Комментариев нет:
Отправить комментарий