A. Jaka jest roznica miedzy (homo)morfizmem grup i (homo)morfizmem pierscieni?
B. Esej o klasyfikacji-terminologii morfizmow.
Homo-morfizm - (grec. homo-podobny, taki samy). Homomorfizm oznacza odwzorowanie jednej struktury algebroicznej w drugą, zachowując przy tym strukturę i odpowiadające sobie operacje. I to odwzorowanie jest podobne do tych struktur algebroicznych.
Endo-morfizm - homomorfizm, który odwzorowuje system algebroiczny w siebie, czyli w swój podsystem. Endo - wewnętrzny.
Epi-morfizm - jednoznaczne odwzorowanie jednego systemu algebraicznego na inny. Posiada prawostronną własność skracania. Epi- prawy.
Mono-morfizm - przekształcenie różnowartościowe, posiada lewostronną własność skracania. Mono- lewy.
Izo-morfizm - morfizm, który posiada lewą i prawą odwrotność, jest jednocześnie epimorfizmem i monomorfizmem, i te odwrotności są równoważne. Izo- równy.
*Morfizm posiada jadro.
*Morfizmy pierscieni NIE mozno dodawac!
Homo-morfizm grup – w teorii grup funkcja odwzorowująca grupę w grupę, czyli przekształcenie zachowujące strukturę tych algebr.
Homo-morfizm pierścieni to, nieformalnie, przekształcenie z jednego pierścienia w drugi zachowujące strukturę.
Niech 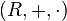 oraz
oraz  będą dowolnymi pierścieniami.
będą dowolnymi pierścieniami.
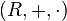 oraz
oraz  będą dowolnymi pierścieniami.
będą dowolnymi pierścieniami.
Homomorfizmem pierścieni  i
i  nazywamy dowolne odwzorowanie
nazywamy dowolne odwzorowanie 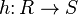 takie, że
takie, że
 i
i  nazywamy dowolne odwzorowanie
nazywamy dowolne odwzorowanie 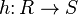 takie, że
takie, że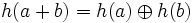 oraz
oraz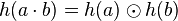 .
.
DefinicjaNiech G, F będą grupami.
(1) Odwzorowanie φ : G → F nazywamy homomorfizmem, jeśli
∀a, b ∈ G[φ(a · b) = f(a) · f(b)].
Zbiór wszystkich homomorfizmów grupy G w grupę F oznaczamy Hom(G, F).
(2) Homomorfizm φ : G → F nazywamy monomorfizmem, jeśli jest różnowartościowy.
(3) Homomorfizm φ : G → F nazywamy epimorfizmem, jeśli jest surjektywny.
(4) Homomorfizm φ : G → G nazywamy endomorfizmem. Zbiór wszystkich endomorfizmów oznaczamy
End(G).
(5) Izomorfizm φ : G → G nazywamy automorfizmem. Zbiór wszystkich automorfizmów oznaczamy
Aut(G).
(6) Jeśli φ : G → F jest homomorfizmem, to zbiór
ker φ = φ−1
(1F ) = {a ∈ G : φ(a)=1F }
nazywamy jądrem homomorfizmu φ, zaś zbiór
imφ = φ(G) = {b ∈ F : ∃a ∈ g[b = φ(a)]}
nazywamy obrazem homomorfizmu φ.
Niech G, F będą grupami, niech φ : G → F będzie homomorfizmem. Wówczas:
(1) φ(1G)=1F ;
(2) φ(a−1)=(φ(a))−1, dla a ∈ G;
(3) φ(ak)=(φ(a))k, dla a ∈ G;
(4) r(φ(a))|r(a), dla a ∈ G;
(5) jeśli φ jest izomorfizmem, to r(φ(a)) = r(a), dla a ∈ G.
Dowód. (1) Mamy:
φ(1G) = φ(1G · 1G) = φ(1G)φ(1G),
skąd, po skróceniu, φ(1G)=1G.
(2) Mamy:
1F = φ(1G) = φ(a · a−1
) = φ(a)φ(a−1
),
skąd, po podzieleniu, φ(a−1)=(φ(a))−1.
(3) Prosty dowód indukcyjny pozostawiamy Czytelnikowi jako nietrudne ćwiczenie.
(4) Niech r(a) = k. Wówczas ak = 1G i stąd
1F = φ(1G) = φ(ak)=(φ(a))k.
Zatem r(φ(a))|r(a).
(5) Odwzorowanie φ : G → F jest różnowartościowe i surjektywne, więc istnieje odwzorowanie
odwrotne φ−1 : F → G. W szczególności
r(φ(a))|r(a) oraz r(φ−1
(φ(a))) = r(a)|r(φ(a)).
Zatem r(φ(a)) = r(a).
B. Esej o klasyfikacji-terminologii morfizmow.
Homo-morfizm - (grec. homo-podobny, taki samy). Homomorfizm oznacza odwzorowanie jednej struktury algebroicznej w drugą, zachowując przy tym strukturę i odpowiadające sobie operacje. I to odwzorowanie jest podobne do tych struktur algebroicznych.
Endo-morfizm - homomorfizm, który odwzorowuje system algebroiczny w siebie, czyli w swój podsystem. Endo - wewnętrzny.
Epi-morfizm - jednoznaczne odwzorowanie jednego systemu algebraicznego na inny. Posiada prawostronną własność skracania. Epi- prawy.
Mono-morfizm - przekształcenie różnowartościowe, posiada lewostronną własność skracania. Mono- lewy.
Izo-morfizm - morfizm, który posiada lewą i prawą odwrotność, jest jednocześnie epimorfizmem i monomorfizmem, i te odwrotności są równoważne. Izo- równy.
*Morfizm posiada jadro.
*Morfizmy pierscieni NIE mozno dodawac!

Комментариев нет:
Отправить комментарий